Sine definition, a cornerstone of trigonometry, embarks on a mathematical journey to unveil the secrets of angles and triangles. Its intricate mathematical expression, graphical representation, and diverse applications across fields like physics and engineering paint a captivating picture of its significance.
From solving trigonometric equations to modeling periodic phenomena, sine definition weaves its way into the fabric of our scientific and technological advancements, leaving an enduring mark on our understanding of the world around us.
Definisi dan Ekspresi Matematika
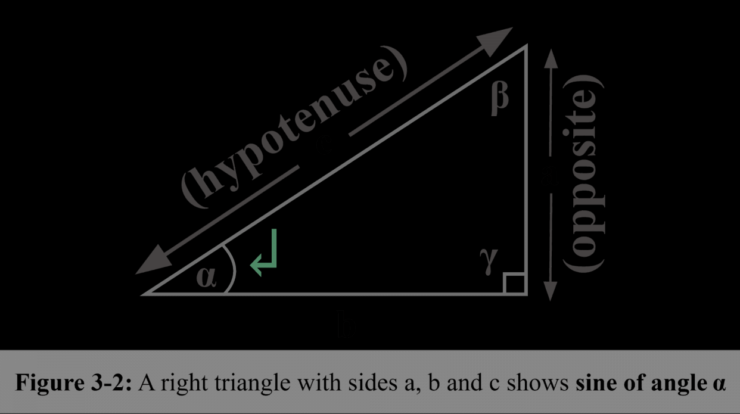
Fungsi sinus adalah fungsi trigonometri yang mewakili rasio sisi yang berlawanan dengan sisi miring dalam segitiga siku-siku.
Ekspresi matematika untuk fungsi sinus adalah:
sin(θ) = sisi berlawanan / sisi miring
Di mana θ adalah sudut yang dibentuk oleh sisi yang berlawanan dan sisi miring.
Range fungsi sinus adalah dari -1 hingga 1, dan domainnya adalah semua bilangan real.
| Sudut (θ) | Sin(θ) |
|---|---|
| 0° | 0 |
| 30° | 1/2 |
| 45° | √2/2 |
| 60° | √3/2 |
| 90° | 1 |
Representasi Grafik
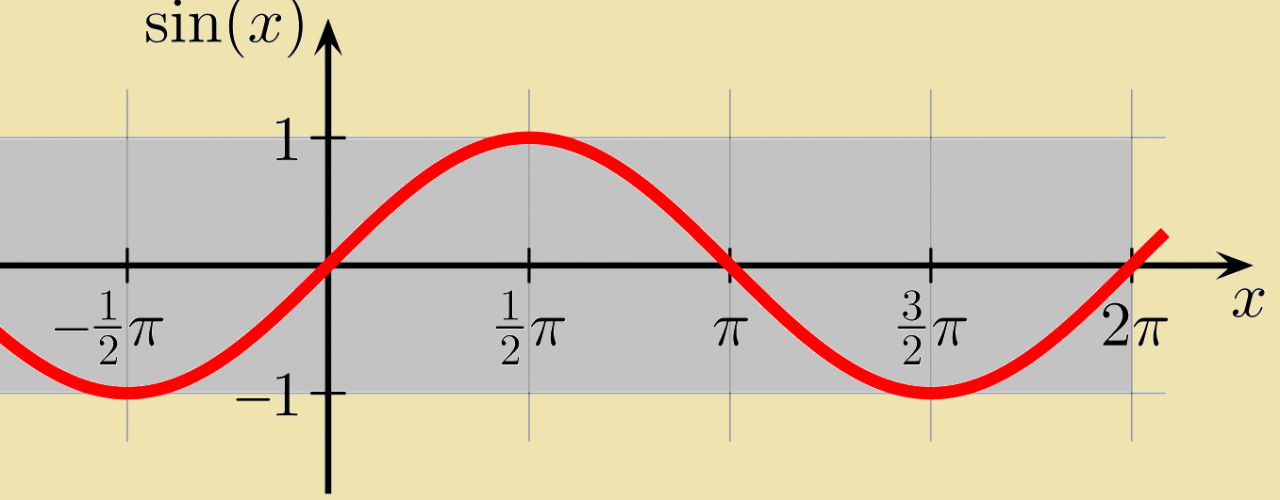
Grafik fungsi sinus adalah gelombang sinusoidal, yang merupakan kurva halus yang berosilasi di sekitar garis x.
Karakteristik gelombang sinusoidal meliputi:
- Amplitudo:Jarak vertikal maksimum dari garis x.
- Periode:Jarak horizontal antara dua puncak atau dua titik terendah yang berurutan.
- Frekuensi:Jumlah periode yang terjadi dalam satu satuan waktu.
Gelombang sinusoidal memiliki banyak aplikasi di dunia nyata, seperti:
- Musik
- Fisika
- Teknik
Aplikasi dalam Trigonometri: Sine Definition
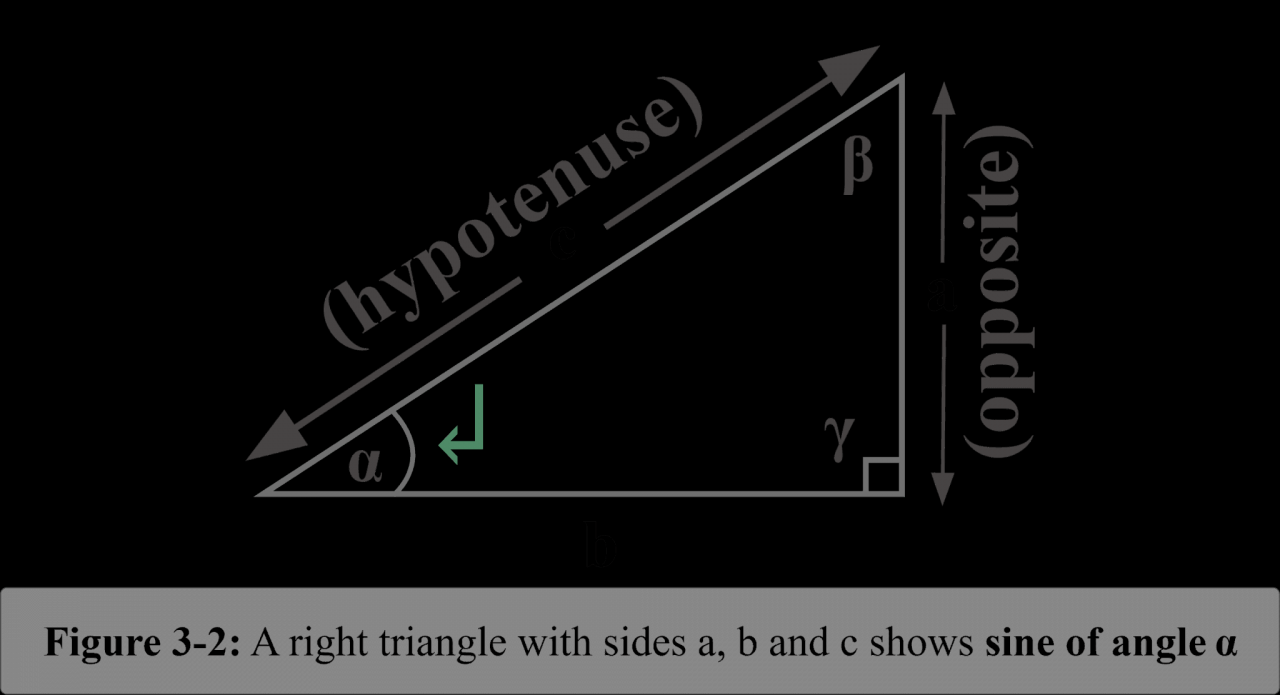
Fungsi sinus digunakan untuk menyelesaikan persamaan trigonometri, seperti:
sin(θ) = a/b
Di mana a adalah sisi yang berlawanan dan b adalah sisi miring.
Fungsi sinus juga digunakan untuk menemukan sisi dan sudut yang hilang dari segitiga, seperti:
sin(A)/a = sin(B)/b = sin(C)/c
Di mana A, B, dan C adalah sudut segitiga, dan a, b, dan c adalah sisi yang berlawanan.
Kalkulus dan Turunan
Turunan dari fungsi sinus adalah:
cos(θ) =
sin(θ)
Turunan fungsi sinus digunakan dalam kalkulus untuk:
- Mencari titik kritis dan ekstrem.
- Mencari interval kenaikan dan penurunan.
- Mencari konveksitas.
Aplikasi dalam Fisika dan Teknik
Fungsi sinus digunakan untuk memodelkan fenomena periodik, seperti:
- Osilasi
- Getaran
- Gelombang
Fungsi sinus juga digunakan dalam teknik listrik, seperti:
- Arus bolak-balik
- Rangkaian resonansi
- Transmisi sinyal
Final Wrap-Up
In conclusion, sine definition stands as a testament to the power of mathematics in unraveling the complexities of our universe. Its versatility and ubiquity make it an indispensable tool for scientists, engineers, and anyone seeking to comprehend the intricate dance of angles and shapes.
Answers to Common Questions
What is the mathematical expression for sine?
The mathematical expression for sine is sin(x) = opposite/hypotenuse, where x is the angle measured from the horizontal.
What is the range and domain of the sine function?
The range of the sine function is [-1, 1], and its domain is all real numbers.
How is sine used in real-world applications?
Sine is used in various real-world applications, including navigation, surveying, modeling periodic phenomena, and electrical engineering.